In the first part of this series, we saw a high-level overview of deep learning, and why Scala is a good fit for building neural networks. We also discussed what a deep learning library should provide, and we looked at a few existing libraries. Now it’s time to build the canonical “Hello, World!” example for deep learning: Classifying handwritten digits.
Creating a neural network
Building a neural network usually consists of the following steps:
- Determine your goal.
- Prepare the training data (collect, preprocess, vectorize etc.).
- Divide the data into training set/cross-validation set/test set for evaluation.
- Create the neural network architecture.
- Define the types, number and size of layers.
- Define other hyperparameters such as loss function, optimizer, or learning rate.
- Train your model on the training data.
- Evaluate your model on the cross-validation set.
- Depending on the results, repeat steps 3-5 with different hyperparameters, or collect more data until you’re satisfied with the results.
- Do a final evaluation on the test set.
In our case, the task is already set: We want to recognize handwritten digits. The second step, data preparation, usually takes most of the effort, but we don’t have to worry about it here because it has already been taken care of. We also simplify evaluation a bit here by using a single test dataset for evaluation and just focus on steps 3 to 5. Usually, you should use the cross-validation set while trying out how well different combinations of hyperparameters work, only doing the final evaluation on the test set.
The MNIST Dataset
The MNIST dataset is an image classification dataset containing handwritten digits. It is a classic dataset often used as the “hello world” dataset for machine learning algorithms.
Due to its popularity, most deep learning libraries already provide code for downloading and vectorizing the dataset, letting us focus on the actual learning task.
MNIST consists of a training set of 60000 black and white pictures sized 28 * 28 pixels and their corresponding digit as well as a test set containing another 10000 samples. It is large enough to be interesting, but still small enough that a you can train a model on a CPU.
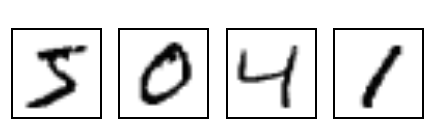
We are going to train a simple neural network on that dataset in each of the libraries in order to get a feeling of what it looks like to work with them. We’ll use a simple neural network architecture called multilayer perceptron (MLP). The following picture shows how our network architecture looks like, conceptually.
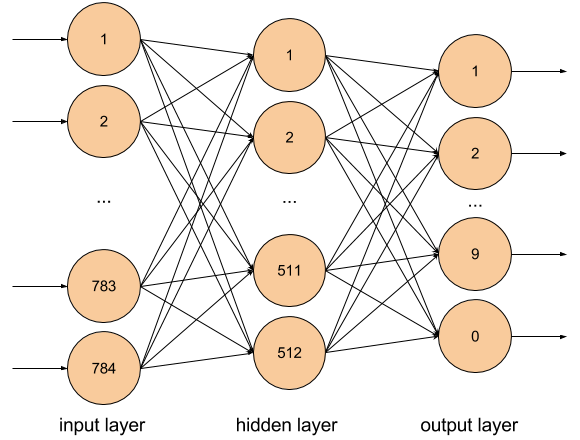
The neurons, denoted by circles, are stacked in layers where each vertical column of neurons represents a layer. The leftmost column is the input layer, the column in the middle is the only hidden layer in our case, and the one on the right represents the output layer.
The arrows show how the inputs of a neuron from one layer are connected to the outputs from the previous layer. As you can see in the image, each input is connected to all the outputs of the previous layer, which is why this type of layer is called a fully connected layer.
Each neuron has a number of weights or parameters, one for each input, whose values are determined during training. As we’ve seen in part one, these weights contain the memory of a neural network, and represent what the network has learned. In our case, how it maps the input image to the a digit.
The input layer just represents the input values and does not have any weights, nor does it do any computation. In our MNIST example the input is the raw pixels of the image, normalized to have a range between zero and one. So we have 28 * 28 input values, represented as a vector of 784 float values.
During a forward pass through the network, each input of a neuron is multiplied by its corresponding weight , and the results of that multiplication are summed up. In our hidden layer, the resulting value is then fed into an activation function called relu that just passes through all positive values but sets any negative number to zero.
In the output layer, we use a softmax function instead, which returns a probability score for each of the 10 classes representing digits. The digit with the highest probability is what the network predicts as image content.
Training a neural network
How do we find a set of weights that works well on new, previously unseen inputs? That’s what training is all about. During training, we take a batch of examples, and run it through our network, starting with random weights. We then compare the output with the correct results, called labels from our examples. More specifically, we compute the difference, or loss, between the two in order to measure how well the network performs. Because the model in our MNIST example predicts the probability of each digit being the content of a given image, a reasonable loss function is the cross entropy loss, which measures the difference between two probability distributions.
We want to minimize the loss in order to get a model that produces predictions close to our training examples. To do that, we calculate the gradient of that loss function with respect to our weights through an algorithm called backpropagation. You can imagine the gradient as being the slope of the loss function for each weight. Backpropagation is basically applying the chain rule (remember calculus?) in order to get the gradient for all weights. Given the gradient, an optimizer such** **as gradient descent changes each weight a little bit in the direction opposite to the gradient, decreasing the loss that way.
Don’t worry If it’s not completely clear to you how gradient descent and backpropagation work. The nice thing about using a neural network library is that it takes care of it for us, hiding the gory details behind a simple API call. If you want to gain a better understanding though, check out the second and third 3blue1brown videos on neural networks.
Evaluation is done on the training data as well as on the test dataset, which contains examples not seen by the network during training. This separation enables us to recognize overfitting, which basically means that the network is memorizing the training examples instead of learning to generalize.
We also have to define how long we want to train the network. A simple way is to just stop after a number of iterations. In our case we we use the number of epochs, that is, how often we run through the entire training set, as a stop criterion. Showing the loss during training can help us to see when it might make sense to stop because we won’t see much enhancement anymore.
MNIST Examples
Now that we’ve designed our neural network, lets finally see some actual code. For the full examples with imports, check out the corresponding project on GitHub.
First, we define our numeric hyperparameters as constants. We’ll use these values in all implementations of our example.
val seed = 42 // fixed random seed for reproducibility
val numInputs = 28 * 28
val numHidden = 512 // size (number of neurons) of our hidden layer
val numOutputs = 10 // digits from 0 to 9
val learningRate = 0.01
val batchSize = 128
val numEpochs = 10DL4J
In DL4J, training and test data is usually fed to the neural network via a DataSetIterator. DL4J already provides a MnistDataSetIterator that takes care of downloading and vectorizing the MNIST dataset.
// download and load the MNIST images as tensors
val mnistTrain = new MnistDataSetIterator(batchSize, true, seed)
val mnistTest = new MnistDataSetIterator(batchSize, false, seed)We define the network architecture and other hyperparameters like the learning rate by creating a NeuralNetConfiguration using the classic Java builder pattern. From that configuration we create a MultiLayerNetwork, which can be used for training.
// define the neural network architecture
val conf = new NeuralNetConfiguration.Builder()
.seed(seed)
.optimizationAlgo(OptimizationAlgorithm.STOCHASTIC_GRADIENT_DESCENT)
.updater(Updater.SGD)
.weightInit(WeightInit.XAVIER) // random initialization of our weights
.learningRate(learningRate)
.list // builder for creating stacked layers
.layer(0, new DenseLayer.Builder() // define the hidden layer
.nIn(numInputs)
.nOut(numHidden)
.activation(Activation.RELU)
.build())
.layer(1, new OutputLayer.Builder(LossFunction.MCXENT) // define loss and output layer
.nIn(numHidden)
.nOut(numOutputs)
.activation(Activation.SOFTMAX)
.build())
.build()
val model = new MultiLayerNetwork(conf)
model.init()
model.setListeners(new ScoreIterationListener(100)) // print the score every 100th iterationTraining the model is just applying the fit method of the network to the training set. We go through our training set of 60000 pictures 10 times.
for (_ <- 0 until numEpochs) {
model.fit(mnistTrain)
}DL4J provides an Evaluation class that can calculate numerous metrics. Here we just print the accuracy of running the model on our training and test set.
// evaluate model performance
def accuracy(dataSet: DataSetIterator): Double = {
val evaluator = new Evaluation(numOutputs)
dataSet.reset()
for (dataSet <- dataSet.asScala) {
val output = model.output(dataSet.getFeatureMatrix)
evaluator.eval(dataSet.getLabels, output)
}
evaluator.accuracy()
}
log.info(s"Train accuracy = ${accuracy(mnistTrain)}")
log.info(s"Test accuracy = ${accuracy(mnistTest)}")Running the example gives us the following output. The score value is the loss value we’re trying to minimize. As you can see, the loss decreases rapidly at first, then starts to flatten out soon. After 10 epochs of training we achieve an accuracy of 92.8% on the test set.
10:41:42.267 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 0 is 2.294145107269287
10:42:31.753 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 100 is 1.4235080480575562
10:43:27.206 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 200 is 1.0206242799758911
10:44:20.751 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 300 is 0.7351394295692444
10:45:09.959 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 400 is 0.7129665017127991
10:46:02.553 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 500 is 0.6167545318603516
...
10:47:38.618 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4200 is 0.34266236424446106
10:47:39.071 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4300 is 0.20224857330322266
10:47:39.483 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4400 is 0.3612464666366577
10:47:39.905 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4500 is 0.24936261773109436
10:47:40.354 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4600 is 0.2355252504348755
10:47:41.767 [main] INFO io.brunk.examples.dl4j.MnistMLP$ - Train accuracy = 0.9259666666666667
10:47:41.905 [main] INFO io.brunk.examples.dl4j.MnistMLP$ - Test accuracy = 0.9282ScalNet
We can download and vectorize the MNIST the same way as with DL4J above.
// download and load the MNIST images as tensors
val mnistTrain = new MnistDataSetIterator(batchSize, true, seed)
val mnistTest = new MnistDataSetIterator(batchSize, false, seed)Defining the network architecture looks quite similar to the Keras API. We create a Sequential model, add our layers to it and then set the global hyperparameters in the call to compile.
// define the neural network architecture
val model: Sequential = Sequential()
model.add(Dense(nOut = numHidden, nIn = numInputs, weightInit = WeightInit.XAVIER, activation = "relu"))
model.add(Dense(nOut = numOutputs, weightInit = WeightInit.XAVIER, activation = "softmax"))
model.compile(lossFunction = LossFunction.MCXENT, optimizer = SGD(learningRate, momentum = 0,
nesterov = true))Training is done through a single call to the fit method, using the number of epochs as argument.
// train the model
model.fit(mnistTrain, nbEpoch = numEpochs, List(new ScoreIterationListener(100)))Evaluation in ScalNet looks almost the same as it does in DL4J.
// evaluate model performance
def accuracy(dataSet: DataSetIterator): Double = {
val evaluator = new Evaluation(numOutputs)
dataSet.reset()
for (dataSet <- dataSet.asScala) {
val output = model.predict(dataSet)
evaluator.eval(dataSet.getLabels, output)
}
evaluator.accuracy()
}
log.info(s"Train accuracy = ${accuracy(mnistTrain)}")
log.info(s"Test accuracy = ${accuracy(mnistTest)}")Running the example gives us an output very similar to our previous example which is not surprising, given that ScalNet uses DL4J internally.
23:13:20.200 [main] INFO o.d.scalnet.models.Sequential - Layer 0: Dense
23:13:20.205 [main] INFO o.d.scalnet.models.Sequential - size: in=List(784) out=List(512)
23:13:20.232 [main] INFO o.d.scalnet.models.Sequential - Layer 1: Dense
23:13:20.233 [main] INFO o.d.scalnet.models.Sequential - size: in=List(512) out=List(10)
...
23:13:24.830 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 0 is 2.294145107269287
23:13:27.563 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 100 is 1.4235080480575562
23:13:30.147 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 200 is 1.0206241607666016
23:13:32.889 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 300 is 0.7351393699645996
...
23:14:54.751 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4300 is 0.20224834978580475
23:14:56.812 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4400 is 0.3612460494041443
23:14:58.639 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4500 is 0.24936220049858093
23:15:00.078 [main] INFO o.d.o.l.ScoreIterationListener - Score at iteration 4600 is 0.23552563786506653
23:15:04.853 [main] INFO io.brunk.examples.scalnet.MnistMLP$ - Train accuracy = 0.9259666666666667
23:15:05.280 [main] INFO io.brunk.examples.scalnet.MnistMLP$ - Test accuracy = 0.9282TensorFlow for Scala
The provided MNISTLoader allows us to download and extract the MNIST dataset. After that, we create a DataSet for training and test data in order to feed the data into the training process.
// download and load the MNIST images as tensors
val dataSet = MNISTLoader.load(Paths.get("datasets/MNIST"))
val trainImages = tf.data.TensorSlicesDataset(dataSet.trainImages)
val trainLabels = tf.data.TensorSlicesDataset(dataSet.trainLabels)
val testImages = tf.data.TensorSlicesDataset(dataSet.testImages)
val testLabels = tf.data.TensorSlicesDataset(dataSet.testLabels)
val trainData =
trainImages.zip(trainLabels)
.repeat()
.shuffle(10000)
.batch(batchSize)
.prefetch(10)
val evalTrainData = trainImages.zip(trainLabels).batch(1000).prefetch(10)
val evalTestData = testImages.zip(testLabels).batch(1000).prefetch(10)First, we define our input shapes. We then build our neural network architecture by composing operations we want to apply to the input data using the >> operator. After defining loss function and optimizer, we create a Model that holds our configuration.
// define the neural network architecture
val input = tf.learn.Input(UINT8, Shape(-1, dataSet.trainImages.shape(1), dataSet.trainImages.shape(2))) // type and shape of images
val trainInput = tf.learn.Input(UINT8, Shape(-1)) // type and shape of labels
val layer = tf.learn.Flatten("Input/Flatten") >> // flatten the images into a single vector
tf.learn.Cast("Input/Cast", FLOAT32) >>
tf.learn.Linear("Layer_1/Linear", numHidden, weightsInitializer = GlorotUniformInitializer()) >> // hidden layer
tf.learn.ReLU("Layer_1/ReLU") >> // hidden layer activation
tf.learn.Linear("OutputLayer/Linear", numOutputs, weightsInitializer = GlorotUniformInitializer()) // output layer
val trainingInputLayer = tf.learn.Cast("TrainInput/Cast", INT64) // cast labels to long
val loss = tf.learn.SparseSoftmaxCrossEntropy("Loss/CrossEntropy") >>
tf.learn.Mean("Loss/Mean") >> tf.learn.ScalarSummary("Loss/Summary", "Loss")
val optimizer = tf.train.GradientDescent(learningRate)
val model = tf.learn.Model(input, layer, trainInput, trainingInputLayer, loss, optimizer)The Estimator is responsible for running the actual training process. We configure it with the model as well as some triggers for checkpoints, logging, and the stop criterion. Training is done with a call the the train method on our estimator.
val accMetric = tf.metrics.MapMetric(
(v: (Output, Output)) => (v._1.argmax(-1), v._2), tf.metrics.Accuracy())
val estimator = tf.learn.InMemoryEstimator(
model,
tf.learn.Configuration(Some(summariesDir)),
// due to a bug, we can't use epochs directly as stop criterion
tf.learn.StopCriteria(maxSteps = Some((60000 / batchSize) * numEpochs)),
Set(
tf.learn.LossLogger(trigger = tf.learn.StepHookTrigger(100)),
tf.learn.Evaluator(
log = true, data = () => evalTrainData, metrics = Seq(accMetric),
trigger = tf.learn.StepHookTrigger(1000), name = "TrainEvaluation"),
tf.learn.Evaluator(
log = true, data = () => evalTestData, metrics = Seq(accMetric),
trigger = tf.learn.StepHookTrigger(1000), name = "TestEvaluation"),
tf.learn.StepRateLogger(log = false, summaryDir = summariesDir, trigger = tf.learn.StepHookTrigger(100)),
tf.learn.SummarySaver(summariesDir, tf.learn.StepHookTrigger(100)),
tf.learn.CheckpointSaver(summariesDir, tf.learn.StepHookTrigger(1000))))
// train the model
estimator.train(() => trainData)We do the final evaluation ourselves, using a function that runs the model on a given set, compares it with the actual labels, and then divides the number of correct predictions by the total number of predictions.
def accuracy(images: Tensor, labels: Tensor): Float = {
val predictions = estimator.infer(() => images)
predictions.argmax(1).cast(UINT8).equal(labels).cast(FLOAT32).mean().scalar.asInstanceOf[Float]
}
// evaluate model performance
logger.info(s"Train accuracy = ${accuracy(dataSet.trainImages, dataSet.trainLabels)}")
logger.info(s"Test accuracy = ${accuracy(dataSet.testImages, dataSet.testLabels)}")2018-01-09 19:52:49.673 [main] INFO Learn / Hooks / Loss Logger - ( N/A ) Step: 0, Loss: 160.4288
2018-01-09 19:52:50.414 [main] INFO Learn / Hooks / Evaluation - Step 0 TestEvaluation: Accuracy = 0.1842
2018-01-09 19:52:51.917 [main] INFO Learn / Hooks / Evaluation - Step 0 TrainEvaluation: Accuracy = 0.1872
2018-01-09 19:52:52.420 [main] INFO Learn / Hooks / Loss Logger - ( 2.750 s) Step: 100, Loss: 1.3103
2018-01-09 19:52:52.866 [main] INFO Learn / Hooks / Loss Logger - ( 0.447 s) Step: 200, Loss: 0.9289
2018-01-09 19:52:53.288 [main] INFO Learn / Hooks / Loss Logger - ( 0.422 s) Step: 300, Loss: 1.5239
2018-01-09 19:52:53.694 [main] INFO Learn / Hooks / Loss Logger - ( 0.405 s) Step: 400, Loss: 1.2546
...
2018-01-09 19:53:13.956 [main] INFO Learn / Hooks / Evaluation - Step 4000 TestEvaluation: Accuracy = 0.8979
2018-01-09 19:53:15.328 [main] INFO Learn / Hooks / Evaluation - Step 4000 TrainEvaluation: Accuracy = 0.9042
2018-01-09 19:53:15.710 [main] INFO Learn / Hooks / Loss Logger - ( 2.054 s) Step: 4100, Loss: 0.3789
2018-01-09 19:53:16.102 [main] INFO Learn / Hooks / Loss Logger - ( 0.391 s) Step: 4200, Loss: 0.4389
2018-01-09 19:53:16.500 [main] INFO Learn / Hooks / Loss Logger - ( 0.399 s) Step: 4300, Loss: 0.3625
2018-01-09 19:53:16.908 [main] INFO Learn / Hooks / Loss Logger - ( 0.408 s) Step: 4400, Loss: 0.4442
2018-01-09 19:53:17.306 [main] INFO Learn / Hooks / Loss Logger - ( 0.398 s) Step: 4500, Loss: 0.8267
2018-01-09 19:53:17.659 [main] INFO Learn / Hooks / Loss Logger - ( 0.353 s) Step: 4600, Loss: 0.1517
2018-01-09 19:53:17.967 [main] INFO Learn / Hooks / Termination - Stop requested: Exceeded maximum number of steps.
2018-01-09 19:53:19.399 [main] INFO io.brunk.examples.MnistMLP$ - Train accuracy = 0.93158334
2018-01-09 19:53:19.723 [main] INFO io.brunk.examples.MnistMLP$ - Test accuracy = 0.9233MXNet
MXNet does not provide binary artifacts for Scala at the moment so we have to compile it ourselves, based on the installation instructions from the project website. We also have to download the MNIST dataset, and extract it into an mnist directory in our project.
MXNet provides an iterator that loads the MNIST dataset and returns batches as tensors. We have to initialize the iterator using a Map[String, String] of key-value pairs.
// load the MNIST images as tensors
val trainDataIter = IO.MNISTIter(Map(
"image" -> "mnist/train-images-idx3-ubyte",
"label" -> "mnist/train-labels-idx1-ubyte",
"data_shape" -> "(1, 28, 28)",
"label_name" -> "sm_label",
"batch_size" -> batchSize.toString,
"shuffle" -> "1",
"flat" -> "0",
"silent" -> "0"))
val testDataIter = IO.MNISTIter(Map(
"image" -> "mnist/t10k-images-idx3-ubyte",
"label" -> "mnist/t10k-labels-idx1-ubyte",
"data_shape" -> "(1, 28, 28)",
"label_name" -> "sm_label",
"batch_size" -> batchSize.toString,
"shuffle" -> "1",
"flat" -> "0",
"silent" -> "0"))The MXNet symbol API allows us to define our neural network architecture. The use of three parameter stems from the fact that it is a very direct port of the Python API. We set most parameters through a Map of key-value pairs.
:::scala
// define the neural network architecture
val data = Symbol.Variable("data")
val fc1 = Symbol.FullyConnected(name = "fc1")()(Map("data" -> data, "num_hidden" -> numHidden))
val act1 = Symbol.Activation(name = "relu1")()(Map("data" -> fc1, "act_type" -> "relu"))
val fc2 = Symbol.FullyConnected(name = "fc3")()(Map("data" -> act1, "num_hidden" -> numOutputs))
val mlp = Symbol.SoftmaxOutput(name = "sm")()(Map("data" -> fc2))Creating the model is done using a builder of the FeedForward class. Here we also set the global hyperparameters. If you have a Nvidia GPU, you can also change the context to gpu in order to speed up training considerably.
:::scala
// create and train the model
val model = FeedForward.newBuilder(mlp)
.setContext(Context.cpu()) // change to gpu if available
.setTrainData(trainDataIter)
.setEvalData(testDataIter)
.setNumEpoch(numEpochs)
.setOptimizer(new SGD(learningRate = learningRate))
.setInitializer(new Xavier()) // random weight initialization
.build()As done in the TensorFlow example, we calculate the accuracy ourselves on both training set and test set by running the model on our test set, and comparing it with the correct labels.
// evaluate model performance
def accuracy(dataset: DataIter): Float = {
dataset.reset()
val predictions = model.predict(dataset).head
// get predicted labels
val predictedY = NDArray.argmax_channel(predictions)
// get real labels
dataset.reset()
val labels = dataset.map(_.label(0).copy()).toVector
val y = NDArray.concatenate(labels)
require(y.shape == predictedY.shape)
// calculate accuracy
val numCorrect = (y.toArray zip predictedY.toArray).count {
case (labelElem, predElem) => labelElem == predElem
}
numCorrect.toFloat / y.size
}
println(s"Train accuracy = ${accuracy(trainDataIter)}")
println(s"Test accuracy = ${accuracy(testDataIter)}")As in the other examples, we achieve an accuracy of 92% after 10 epochs.
17:17:43.033 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[0] Train-accuracy=0.75642693
17:17:43.033 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[0] Time cost=1864
17:17:43.126 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[0] Train-accuracy=0.86478364
17:17:44.678 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[1] Train-accuracy=0.87207866
17:17:44.678 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[1] Time cost=1552
17:17:44.770 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[1] Train-accuracy=0.89252806
17:17:46.437 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[2] Train-accuracy=0.89007413
17:17:46.437 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[2] Time cost=1667
17:17:46.577 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[2] Train-accuracy=0.90134215
...
17:17:57.974 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[8] Train-accuracy=0.9203726
17:17:57.974 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[8] Time cost=1669
17:17:58.088 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[8] Train-accuracy=0.9240785
17:17:59.959 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[9] Train-accuracy=0.9228599
17:17:59.959 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[9] Time cost=1871
17:18:00.075 [run-main-0] INFO ml.dmlc.mxnet.Model - Epoch[9] Train-accuracy=0.9263822
Train accuracy = 0.9240785
Test accuracy = 0.9263822Discussion
After having created and trained an example with each of the libraries, you might ask, which one should you should choose to start a deep learning project? While this decision depends a lot on your goal and context, let’s discuss a few pros and cons I’ve encountered.
DL4J is the oldest and to my impression it is also the most mature library. It covers most common network types, has comprehensive documentation, and also offers commercial support. If you want to use deep learning in production now, DL4J should be a good choice.
There’s still much room for improvements, though. For instance, ND4J is a bit limited when it comes to data types. It only supports float and double, and not both at the same time. You have to decide which one via a global switch. It also does not offer a native Scala API, leaving some of Scala’s advantages we discussed in the motivation to be desired.
This gap naturally leads to ScalNet, which looks promising, but needs more time to mature before it will be actually useful. For instance, it currently does not support any other optimizer besides gradient descent.
I feel a little bit ambivalent about MXNet. While not as mature as DL4J, it seems stable, and having the Scala API being part of the main project is definitely a plus. The API does feel a bit foreign, though, and does not make much use of Scala’s features. For instance, the Symbol API is more or less a direct translation of the Python API, is quite stringified and thus not very type safe. So there’s room for improvement here. Some of the MXNet APIs like the NDArray and IO API are not on par yet with their Python counterpart, i.e. there’s limited slicing on tensors, and no shuffling of inputs. The documentations contains some tutorials, and there are also a few example projects. ScalaDoc is basically empty though, which might stem from the fact that many classes are generated from the C++ sources.
TensorFlow for Scala is the most “scalaesque” of the libraries presented. It offers a mostly functional, immutable API, and it uses Scala’s advanced type system to provide type safety where possible. With some exceptions, i.e heavy usage of nulls, developing with it feels like writing idiomatic Scala most of the time. It also profits from TensorFlow upstream, which has a lot of momentum at the moment, and is used at Google in production from large scale backend to mobile. This means new research results are added fast, and lots of pretrained models are available, but it’s also well tested.
Development of TensorFlow for Scala has started only in 2017, and it’s made impressive progress since. There are still some rough edges though, and it needs much more testing, having many bugs still lurking around. Some introductory documentation exists, although incomplete. It has comprehensive ScalaDoc, something I wish more Scala libraries had.
Conclusion
Now we’ve seen how it looks like to train a very simple neural network in each of the libraries presented. Without any tuning, it is able to recognize handwritten digits with an accuracy of ~92%. With some enhancements, we could do even better, improving accuracy up to 99%. In research, MNIST is basically considered a solved problem, and the focus lies on more interesting challenges.
What we’ve done is course a very simple example, and we’ve barely scratched the surface of what’s possible with deep learning and with the libraries presented. To keep things simple, we haven’t touched many topics, for instance
- other types of neural networks, like convolutional neural networks (CNN), recurrent neural networks (RNN), or generative adversarial networks (GAN)
- how to avoid overfitting
- data science tools such as notebooks
- visualization
- distribution (multi gpu and multi host)
As you can see, there’s much more to explore. I hope I can show you more interesting applications of deep learning in future blog posts. If you have any questions or feedback, don’t hesitate to leave a comment, or ping me on Twitter @soebrunk.